
Histogram of total stopping times for the numbers 1 to 10 9. Total stopping time is on the x axis, frequency on the y axis. Statement of the problem Numbers from 1 to 9999 and their corresponding total stopping time Histogram of total stopping times for the numbers 1 to 10 8. Paul Erdős said about the Collatz conjecture: "Mathematics may not be ready for such problems." Jeffrey Lagarias stated in 2010 that the Collatz conjecture "is an extraordinarily difficult problem, completely out of reach of present day mathematics". The sequence of numbers involved is sometimes referred to as the hailstone sequence, hailstone numbers or hailstone numerals (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers. It is also known as the 3 n + 1 problem (or conjecture), the 3 x + 1 problem (or conjecture), the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem.


It is named after the mathematician Lothar Collatz, who introduced the idea in 1937, two years after receiving his doctorate. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence.
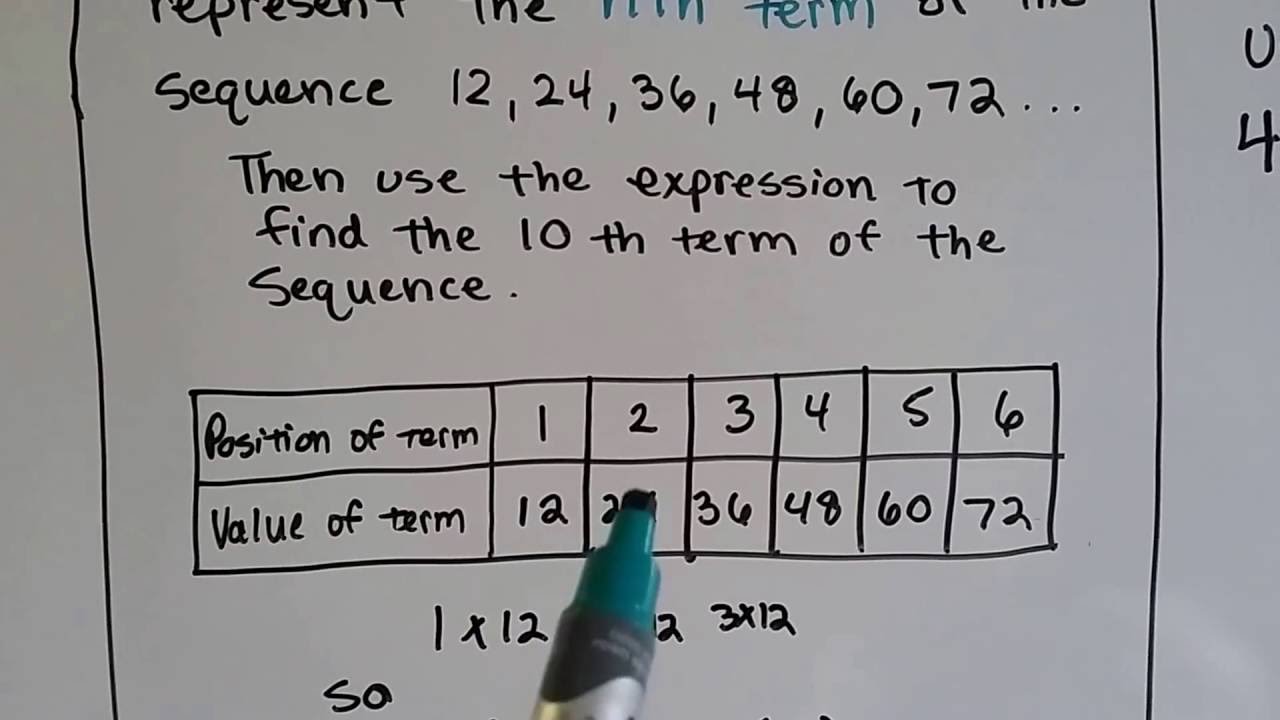
SEQUENCES MATH QUESTION PLUS
If the previous term is odd, the next term is 3 times the previous term plus 1. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even, the next term is one half of the previous term. The conjecture asks whether repeating two simple arithmetic operations will eventually transform every positive integer into 1. The Collatz conjecture is one of the most famous unsolved problems in mathematics. The Collatz conjecture states that all paths eventually lead to 1. So using a different method, we’ve found that the number of pills will be zero in the sixth week, which confirms that the patient will stop taking the medicine completely in the sixth week.(more unsolved problems in mathematics) Directed graph showing the orbits of small numbers under the Collatz map, skipping even numbers.

We then add one to each side of the equation giving 𝑛 equals six. We can then divide both sides of the equation by three, giving one multiplied by 𝑛 minus one or simply 𝑛 minus one is equal to five. To find the week in which the patient will stop taking the medicine completely, we can set the general term equal to zero, because that represents the number of pills, and then solve the resulting equation to find 𝑛, the term number.įirst, we can add three multiplied by 𝑛 minus one to each side, giving three multiplied by 𝑛 minus one is equal to 15. So the formula for the general term is 𝑎 sub 𝑛 equals 15 minus three multiplied by 𝑛 minus one. The first term in this sequence is 15, and the common difference is negative three. And 𝑑 represents the common difference between the terms. 𝑎 or sometimes 𝑎 one represents the first term. The general term of an arithmetic sequence is given by 𝑎 sub 𝑛 equals 𝑎 plus 𝑛 minus one 𝑑, where 𝑎 sub 𝑛 represents the 𝑛th term. And so this is an example of an arithmetic sequence. As the terms decrease by the same amount each time, this means the difference between successive terms is constant. So in the sixth week, the patient will stop taking the medicine completely.Īnother way to approach this problem would be to find a formula for the general term in the sequence. In the fourth week, the patient will take nine minus three, which is equal to six pills in the fifth week, six minus three, which is three pills and finally, in the sixth week, three minus three, which is zero. So we need to continue like this until we get to zero pills. We want to find the week in which the patient will stop taking the medicine completely. In the third week, they’ll take three less again, 12 minus three which is equal to nine, so nine pills in the third week. That means in the second week, they should take three less than 15, 15 minus three which is equal to 12. The patient should then decrease the dosage, that means the number of pills they take, by three pills every week. We’re told in the question that the doctor prescribed 15 pills for the patient to take in the first week. Given that the patient should decrease the dosage by three pills every week, find the week in which he will stop taking the medicine completely. A doctor prescribed 15 pills for his patient to be taken in the first week.


 0 kommentar(er)
0 kommentar(er)
